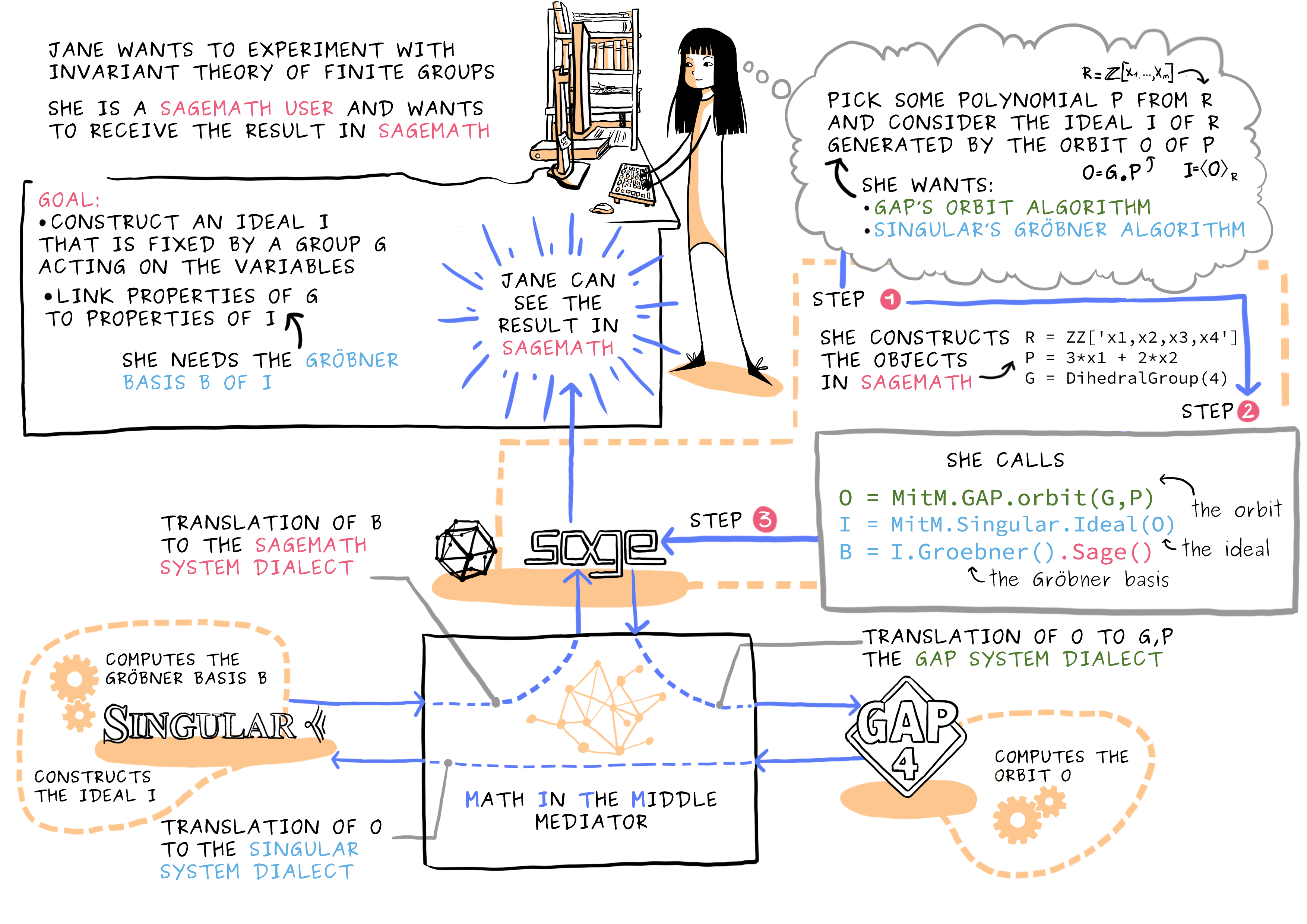
The comic above shows off the idea of an interoperability layer for mathematical software systems base on the Math-in-the-Middle (MitM) paradigm using a combination of Singular, Sage and GAP. In this blog post, we detail another use case with the computer algebra systems SageMath and Pari, but now with the mathematical database LMFDB in the mix.
This use case is important, since exploring mathematical data sets often requires both data base operations and computation: mathematical data bases like LMFDB, the OEIS, or FindStat are conceptually condensed tabulations of prior computations that can be searched over for completeness.
The use case described here is about Modular Forms, a class of objects of immense importance in number theory and cryptography.
In a nutshell: The LMFDB contains many individual instances of several kinds of modular forms (which are the “MF” in the LMFDB). Each of these objects has associated to it an algebraic number field called its Hecke field. A mathematically interesting project is to study these Hecke fields for the modular forms in each collection, collecting data about them such as their degree or class number (see the next section for definitions) and investigating how these are distributed. Being able to access this LMFDB data directly from within a package with the ability to carry out its own computations with number fields would be a useful application.
To conduct this research, we need a tight two-ways integration between the LMFDB and computational systems like SageMath or Pari. But as the LMFDB, SageMath and PARI are separate systems, designed with differing application areas and constraints in mind, this integration is non-trivial on several levels. This is where the Math-in-the-Middle Paradigm comes to the rescue.
Systems (A, …, H in the image) are connected via formal representations their APIs (data types and functions), which are in turn related to a central (system-independent) mathematical ontology: the Math-in-the-Middle Ontology. In the OpenDreamKit implementation of the MitM Paradigm, the system APIs and the MitM Ontology are implemented as OMDoc/MMT theory graphs.
At the system level, SageMath (or PARI) and LMFDB are connected via a MitM Mediator, which receives requests from SageMath (in terms of the SageMath API), translates them to the LMFDB API via their relations to the MitM Ontology, and back.
In essence, the knowledge about the connections between the system API theories and the MitM Ontology acts as semantic glue between the systems.
John Cremona and David Lowry-Duda wrote up a detailed mathematical use case for integrating LMFDB with SageMath and/or Pari/GP via the virtual theories in MMT and the Math-in-the-Middle Paradigm.
Based on this document, work on fully realizing this use case is ongoing; the next steps are:
- the KWARC group at FAU work on the virtual theories for the tables involved in collaboration with the LMFDB group at Warwick.
- the UPSud group extends the SAGE interface theories to cover the necessary interface functions.
- we (together) make sure that the Math-in-the-Middle ontology has the necessary theories (at least as stubs) and alignments.
SageMath WP6: Data/Knowledge/Software bases Math-in-the-Middle Use Cases Open Science and Reproducibility Pari/GP LMFDB